During Thanksgiving Break I played the card game War with my girlfriend and remembered how wonderfully mindless it is. Because there’s no strategy or decision-making, it was feasible to write a program to play the game. Once I could simulate one game, I could simulate several and collect some statistics.
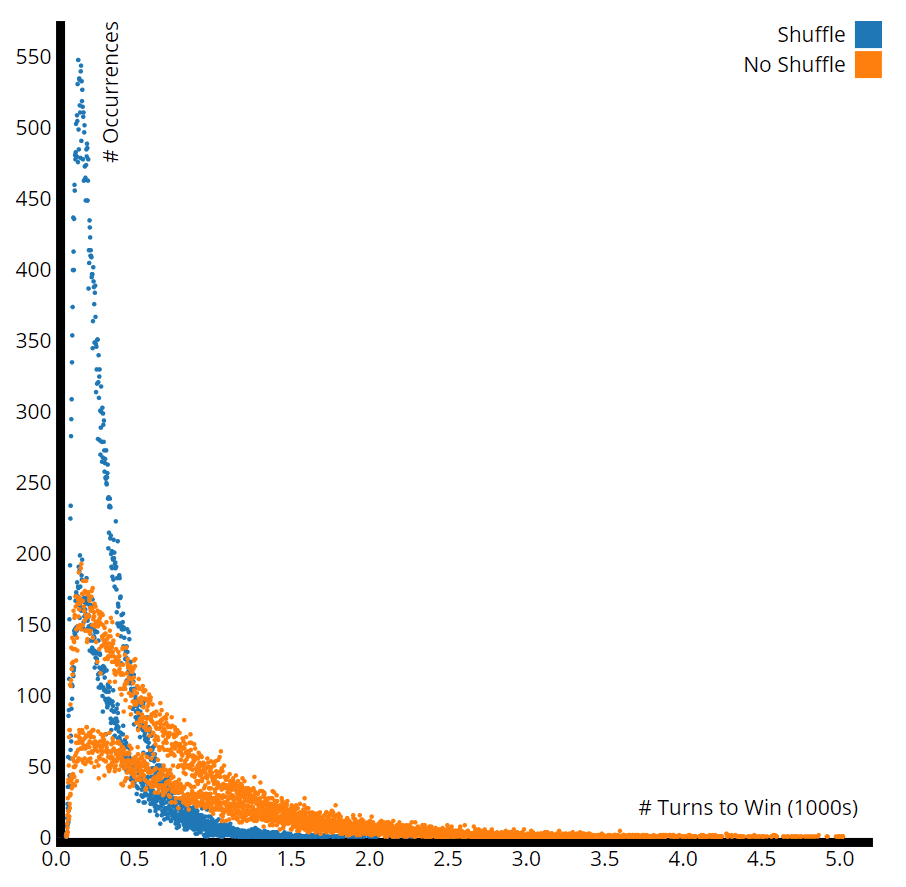
Evidently the rules of War have some gaps, including what to do with the cards you win. Do you place them on the bottom of your deck, in order, or do you shuffle and reuse them once your deck is empty? Why not program both methods and compare? Here is a plot of both approaches after 100,000 trials of each. The x-axis is the number of turns required to complete the game, and the y-axis is the frequency of that outcome across 100,000 trials.
The data proved more interesting than I expected.
- Shuffling the winnings led to much faster games — a mean of 262, a mode of 84, and a max of 2,702 turns.
- When the winnings aren’t shuffled, the numbers are less clear. Many games were seemingly infinite so I added a cap of 5,000 turns per game. 11,837 (11.8%) of the games hit this limit (and do not appear on the graph). But plenty of games ended after 4,000+ turns, so we could expect many of these long games to be finite as well. If we ignore the capped games, the mode is 104 turns.
- Both plots show a binary distribution of the results, as you can see in the higher and lower groupings of dots. It turns out that games are more likely to finish after an even number of turns. Each player starts with 26 cards, so if there are no wars and one player wins every hand, the game will last 26 turns. For every turn that player loses, they must win an additional hand to cancel the loss, so the game still requires an even number of turns. Only a war will break this trend because 4 cards change possession instead of 1. A game with an odd number of wars will take an odd number of turns to complete (ignoring wars with fewer than 3 cards, when one player’s deck is low).
As for the program, here it is in JavaScript. The highlighted lines show the changes made between the Shuffle and No-Shuffle versions.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 |
(function() { var NUM_TRIALS = 100000, // # games to simulate MAX_TURNS = 5000; // maximum # of turns to avoid infinite loops // From http://stackoverflow.com/a/2450976 function shuffle(array) { var currentIndex = array.length, temporaryValue, randomIndex ; // While there remain elements to shuffle... while (0 !== currentIndex) { // Pick a remaining element... randomIndex = Math.floor(Math.random() * currentIndex); currentIndex -= 1; // And swap it with the current element. temporaryValue = array[currentIndex]; array[currentIndex] = array[randomIndex]; array[randomIndex] = temporaryValue; } return array; } function Card(o) { var self = this; self.suit = o.suit; self.value = o.value; // Generate a string representation of the card self.toString = function() { var displayValue = self.value; switch(self.value) { case 11: displayValue = 'J'; break; case 12: displayValue = 'Q'; break; case 13: displayValue = 'K'; break; case 14: displayValue = 'A'; break; } return self.suit + displayValue; }; // Return a negative number if compare is higher than this card. // Return a positive number if this card is higher than compare. // Return zero if the cards are equal. self.compare = function(/*Card*/ compare) { return self.value - compare.value; }; return self; } function Player(o) { var self = this, hand = [], discard = []; self.name = o.name || 'Player'; // Draw one card from the player's hand self.draw = function() { if(hand.length === 0) { // Version 1: The discard pile is shuffled before using //hand = shuffle(discard).concat(hand); // Version 2: The discard pile is used in the order that it was created hand = discard.concat(hand); discard = []; } return hand.pop(); }; // Add one or more cards to the player's discard pile self.discard = function(cards) { if(Array.isArray(cards)) { discard = cards.concat(discard); } else { discard.push(cards); } }; // Count the total number of cards in this player's possession self.numCards = function() { return hand.length + discard.length; }; // Does the user have any cards remaining? self.hasCards = function() { return self.numCards() > 0; }; // Generate a string representation of the player self.toString = function() { return self.name + ' (' + self.numCards() + ' cards)'; }; return self; } function Game(o) { var self = this, deck = shuffle(o.deck); // The number of turns that have elapsed in this game self.numTurns = 0; // Simulate a single game self.play = function() { var player1 = new Player({ name: 'John' }), player2 = new Player({ name: 'Jane' }); // Split the deck between the two players var iDeck; for(iDeck = 0; iDeck < deck.length; iDeck++) { if(iDeck % 2) { player1.discard(deck[iDeck]); } else { player2.discard(deck[iDeck]); } } var player1Card, player2Card, cardCompare, winnings, isWar, numWarCards, iWarCards; while(player1.hasCards() && player2.hasCards()) { self.numTurns++; // End this game if it's taking too long, to avoid potentially infinite loops if(self.numTurns > MAX_TURNS) { return; } player1Card = player1.draw(); player2Card = player2.draw(); winnings = [ player1Card, player2Card ]; cardCompare = player1Card.compare(player2Card); if(cardCompare > 0) { // Player 1 wins this turn player1.discard(winnings); } else if(cardCompare < 0) { // Player 2 wins this turn player2.discard(winnings); } else { // War! do { // If a player is completely out of cards now, they lose the game if(!player1.hasCards()) { // Player 2 wins this game isWar = false; player2.discard(winnings); } else if(!player2.hasCards()) { // Player 1 wins this game isWar = false; player1.discard(winnings); } else { isWar = true; // If either player doesn't have enough cards for war, bet what they have numWarCards = Math.min(player1.numCards() - 1, player2.numCards() - 1, 3); for(iWarCards = 0; iWarCards < numWarCards; iWarCards++) { winnings.push(player1.draw()); winnings.push(player2.draw()); } player1Card = player1.draw(); player2Card = player2.draw(); winnings.push(player1Card); winnings.push(player2Card); cardCompare = player1Card.compare(player2Card); if(cardCompare > 0) { // Player 1 wins the war and this turn isWar = false; player1.discard(winnings); } else if(cardCompare < 0) { // Player 2 wins the war and this turn isWar = false; player2.discard(winnings); } else { // The card values are equal again, continue the war } } } while(isWar); } } // Note: this is erroneous if MAX_TURNS was reached self.winner = player1.hasCards() ? player1 : player2; }; return self; } // Generate the master deck of all 52 cards. // It will be reused and shuffled in each Game instance. var suits = [ '♠', '♣', '♥', '♦' ], deck = []; var iSuit, iValue; for(iSuit = 0; iSuit < suits.length; iSuit++) { // J = 11, Q = 12, K = 13, A = 14 for(iValue = 2; iValue <= 14; iValue++) { deck.push(new Card({ suit: suits[iSuit], value: iValue })); } } // Run the desired number of trials. // Populate wins with the number of turns and frequency of that outcome. var iTrials, thisGame, wins = []; for(iTrials = 0; iTrials < NUM_TRIALS; iTrials++) { thisGame = new Game({ deck: deck }); thisGame.play(); if(!wins[thisGame.numTurns]) { wins[thisGame.numTurns] = 1; } else { wins[thisGame.numTurns]++; } } }()); |
To close, enjoy the amazing uniqueness of a well-shuffled deck.
I know this is an older post but I just wanted to say thank you! I was assigned the task of creating a program that could simulate a game of war and I designed it to not shuffle. Seeing the statistics laid out like this made it much easier to determine if my game lengths were falling in line with what you may expect from a typical game. The frequency of an endless game being played threw me off and I honestly thought there was something wrong with my code until I took a look at your data. Is the act of shuffling a common rule? Where I live everyone I have ever played with typically adds their winnings to the bottom of their pile as we go along. Thanks again!
Thanks Benjamin! I’m glad this old post could help you.
When I learned to play War, we shuffled. I think this adds excitement to the game. My fiancée learned to play without shuffling, and so perhaps it’s no coincidence that she considers War a waste of time. The Wikipedia article seems to confirm that the rules are hazy on this point.
In any event, this simulation was eye-opening for me and I’d definitely recommend shuffling to anyone who wants a quicker game. But then again, I remember as a kid playing War with my brothers during neverending car trips. Stretching out every game by not shuffling might be a better way to pass the time.